Code

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

df = pd.read_csv(
    "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
)

df.Month = pd.DatetimeIndex(df.Month, freq="MS")
df = df.set_index("Month")

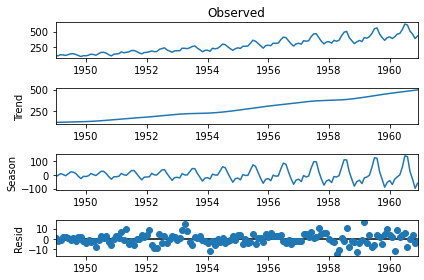
Decomposition

Time series can be thought of as made up of in a few components. Specifically:

\(S_{t}\): Seasonal component
\(T_{t}\): Trend component
\(R_{t}\): Remainder component

These few components can be put together a few ways, but there are two ways that are common:

Additive decomposition
Multiplicative decomposition

Additive Decomposition

\[ y_{t} = S_t + T_t + R_t \]

This is relatively easy to understand when we make an additive time series. Here’s an intuitive(-ish) example:

Code

t = np.linspace(-2 * np.pi, 2 * np.pi)
s_t = np.sin(2 * t)
t_t = np.linspace(start=1, stop=len(t) / 5, num=len(t))
r_t = np.random.randn(len(t))

plt.figure(figsize=(14, 7))
plt.title("Additive Time Series")
plt.plot(t, s_t + t_t + r_t, label="Combined Value")
plt.xlim(left=min(t), right=max(t))
plt.legend()
plt.show()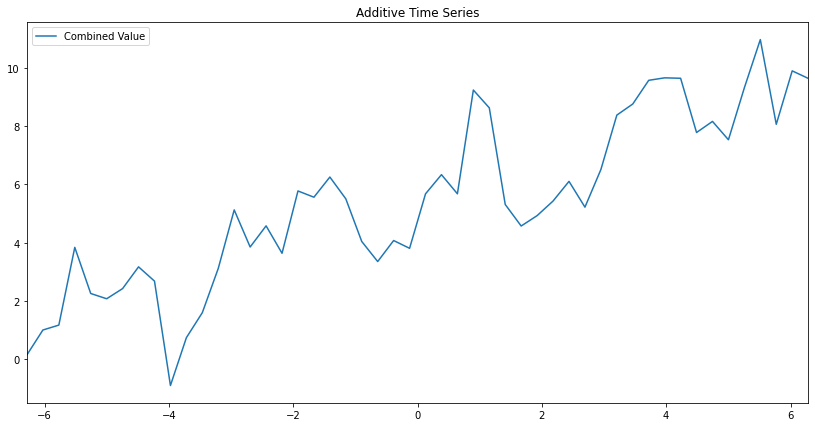

Below we can actually see the separate components I used to make this plot! Notice how each of the series added together creates the final plot above. That’s additive seasonal decomposition in a nutshell. Finding those components.

Code

fig, ax = plt.subplots(nrows=3, ncols=1, figsize=(14, 7), sharex=True)
ax[0].plot(t, s_t, label=r"$S_{t}$", color="blue")
ax[1].plot(t, t_t, label=r"$T_{t}$", color="red")
ax[2].plot(t, r_t, label=r"$R_{t}$", color="green")

ax[0].set_xlim(left=min(t), right=max(t))

ax[0].set_title(r"Seasonal Pattern ($sin(2*t)$)")
ax[1].set_title("Trend")
ax[2].set_title("Remainder")
fig.legend()
plt.show()

Multiplicative Decomposition

Multiplicative decomposition is the same as additive (in a way) but with multiplication. I know, shocking. Ridiculously shocking.

\[ y_{t} = S_t * T_t * R_t \]

There’s one thing to note that actually is interesting. There’s an increase in the variance from what we see as “trend”.

Code

plt.figure(figsize=(14, 7))
plt.title("Multiplicative Time Series")
plt.plot(t, s_t * t_t, label="Combined Value", color="blue")
plt.axhline(y=0, linestyle="--", color="grey")
plt.xlim(left=min(t), right=max(t))
plt.legend()
plt.show()

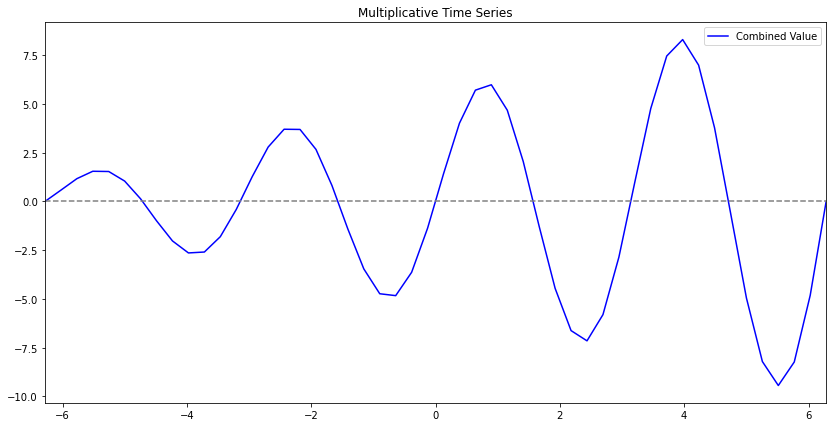
Keep in mind the components are exactly the same as previously.

from statsmodels.tsa.seasonal import STL
from statsmodels.tsa.seasonal import seasonal_decompose

model = seasonal_decompose(x = df['Passengers'], model = 'multiplicative')

stl = STL(df)
res = stl.fit()
fig = res.plot()